6.1 Other Collections
이제껏 리스트에 대해서 알아보았다. 이번 챕터에서는 리스트 외에도 스칼라의 기본적인 컬렉션(Seq, Set, Map)에 대해 알아보도록 하자.
Vector
리스트의 경우에는 첫번째 element 에 접근하는게 마지막 element 에 접근하는 것보다 훨씬 빠르다. 리스트의 구조가 트리 형태로 구성되어 있고 우측으로 갈수록 트리의 깊이가 깊어지기 때문에 그렇다. 이에 반해 Vector 는 리스트 보다 access pattern 이 훨씬 균형잡혀 있다.
벡터는 최초에 2^5(32 개)의 원소를 가지는 array 가 만들어 진다. 32 개가 넘는 원소가 필요하게 되면, 그다음은 32 개를 추가로 만드는 것이 아니라, 2^5 * 2^5 개, 그러니깐 총 2^10(1024 개)의 원소가 들어갈 수 있는 리스트가 추가로 만들어 지는 것이다. 왜 이런식으로 커질까? 원소가 32 개보다 커지면, 처음 만들어진 32 개짜리 벡터는 각각의 32 개짜리 원소를 가지는 벡터의 포인터가 되고 그 아래로 각각 벡터가 만들어진다. 즉, 처음 32 개짜리 원소에서 1024 개를 담을 수 있는 벡터로 바뀌게 된다. 그렇기 때문에 어떤 값을 찾는데 log32(N) 시간만 소요된다. 리스트보다 훨 낫다.
또 다른 장점으로는 map, for, filter, fold 와 같은 연산(bulk operations)이 빠르다는 것이다. 왜냐하면 벡터는 리스트와 달리 원소가 32 개가 하나의 묶음이다보니 a single cache line 에 위치하기 때문에 접근이 훨씬 빠를것이기 때문이다. 즉 list 는 vector 에 비해서 locality 가 나쁘다고 할 수 있다.
vector 가 이렇게 좋다는데, list 를 써야하는 이유는 무엇일까? recursive data structure 의 head 를 취하고 나머지를 다시 연산하는 모델 안에서는 list 가 훨씬 쉽다. 왜냐하면 한 노드에 하나의 아이템만 존재하기 때문에 head 를 취하기가 훨씬 쉽기 때문이다. 하지만 vector 의 경우 depth 가 1 일때는 몰라도 depth 가 1 만 더 증가해도 훨씬 복잡해진다.
list 의 concat 연산 (::)은 vector 에서 다음과 같이 쓰인다.
x +: xs // xs 앞에 x를 포함하는 새로운 벡터를 붙인다.
xs :+ x // xs 뒤에 x를 포함하는 새로운 벡터를 붙인다.벡터 또한 immutable 하기 때문에 위의 연산을 처리하기 위해서는 기존의 벡터를 새롭게 만들어지는 벡터와 함께 새로운 포인터에 연결해야한다. root 까지 새로운 포인터로 연결이 되고 나면 연산이 완료된다.
Collection Hierachy
스칼라의 collection 은 크게 세가지로 나뉘는데, 하나는 지금껏 살펴봤던 List 와 Vector 가 속하는 Seq, 나머지는 Set 과 Map 이다.
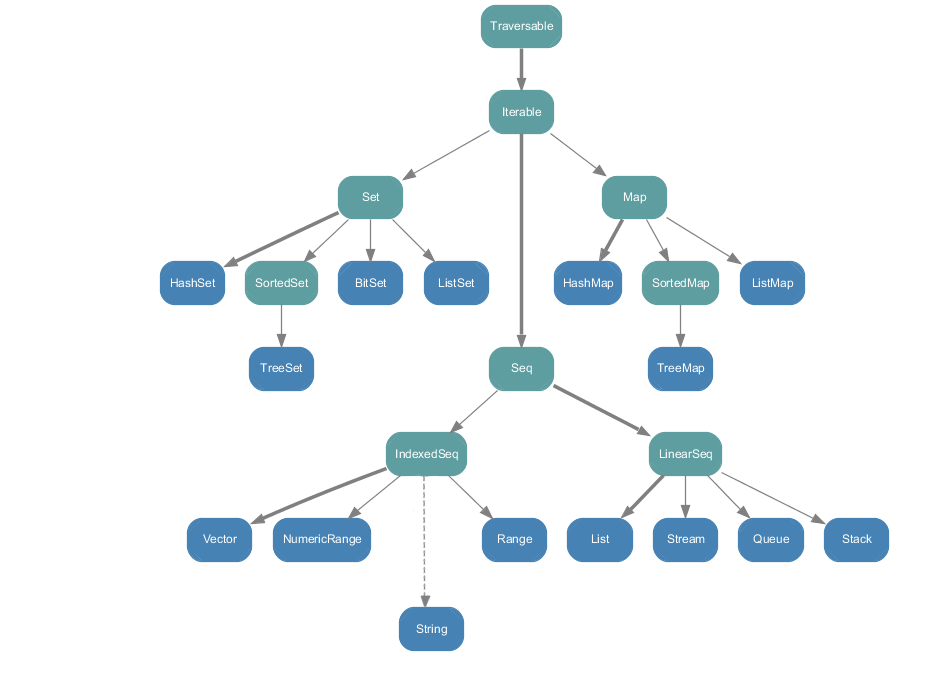
Array 와 String 는 점선으로 되어있는데, 이들도 Seq 로써 아래와 같이 똑같이 동작한다. 다만 자바에서 가져온 타입이기 때문에 앞으로 어떻게 될지(Scala.sequence.String 같은걸 누군가 만들지도 모르므로..) 몰라 점선으로 연결해놓은거 같다.
// Array
val xs = Array(1, 2, 3, 44)
xs map (x => x * 2)
// res0 : Array[Int] = Array(2, 4, 6, 88)
// String
val s = "Hello World"
s filter (c => c.isUpper)
// res1: String = HWRange
Range 는 심플한 seq 타입이다. 사용법 또한 매우 간단하다.
val r: Range = 1 until 5 // 1, 2, 3, 4
val s: Range = 1 to 5 // 1, 2, 3, 4, 5
1 to 10 by 3 // 1, 4, 7, 10
6 to 1 by -2 // 6, 4, 2Some more Sequence Operations
- xs exists p : p 함수의 조건을 만족하는 원소가 있는지
- xs forall p : 모든 원소가 p 함수의 조건을 만족하는지
- xs zip ys : 두 collection 의 원소를 pair 로 가지는 새로운 collection 생성, 타입은 xs
- xs.unzip : zip 형태의 collection 을 분해해서 List 의 tuples 을 만듦, Array 는 안되는군각 요소(xy: pair)의 첫번째와 두번째 요소를 곱한다음 모든값을 sum 해준다.
- xs.flatMap f : 모든 element 에 collection-valued functino f 를 적용
- xs.sum : numeric collection 의 요소들의 합
- xs.product : numeric collection 의 요소들의 곱
- xs.max : 최고값
- xs.min : 최소값
Scalar Product
val a: Vector[Double] = Vector(1.0, 2.0, 3.0)
val b: Vector[Double] = Vector(3.0, 4.0, 5.0)
def scalarProduct(xs: Vector[Double], ys: Vector[Double]): Double =
(xs zip ys).map(xy => xy._1 * xy._2).sum
scalarProduct(a, b)
def scalarProduct2(xs: Vector[Double], ys: Vector[Double]): Double =
(xs zip ys).map{ case (x, y) => x * y }.sum
scalarProduct2(a, b)두 벡터의 각 요소끼리 곱한다음 모든 값을 합하는 함수이다. 우선 xs 와 ys 를 zip 으로 묶은 다음 각 요소(xy: pair)의 첫번째와 두번째 요소를 곱한다음 모든값을 sum 해준다. map 안의 함수는 case 문으로 대체할 수 있다.
{case p1 => e1 ... case pn => en}
// 위와 동일
x => x match { case p1 => e1 ... case pn => en }isPrime
def isPrime(n: Int): Boolean = (2 until n) forall (x => (n % x) != 0)2 부터 n 전까지의 수가 모두 n 으로 나누어 떨어지지 않으면 n 을 prime number(소수)라 할 수 있다.
6.2 Combinatorial Search and For-Expressions
양수 n 이 있고, 또다른 양수 i 와 j 가 1 <= j < i < n 을 만족하고 i + j 가 소수라는 조건이 있다. 코드로 나타내면 다음과 같다.
val n = 7
(1 until n) map (i => (1 until i) map (j => (i, j)))
// result
res0: scala.collection.immutable.IndexedSeq[scala.collection.immutable.IndexedSeq[(Int, Int)]] = Vector(Vector(), Vector((2,1)), Vector((3,1), (3,2)), Vector((4,1), (4,2), (4,3)), Vector((5,1), (5,2), (5,3), (5,4)), Vector((6,1), (6,2), (6,3), (6,4), (6,5)))음.. 분명 Range 타입을 사용하였는데 결과는 Vector of Vectores 가 나왔다. Range 는 Seq 의 하위 타입이지만 사실 그 중간에 IndexedSeq 라는 타입이 존재한다. 결과값으로 pair 가 나왔으므로, Range 타입에는 결과값을 담을 수 없다. 그래서 일단 바로 위의 상위 타입인 IndexedSeq 타입 중에서 pair 를 담을 가장 적합한 타입인 Vector 가 선택되어 나타난것이다.
원래 우리가 찾으려고 했던 결과는 Vector 의 Vector 가 아니라 pair 를 하나의 single list 에 담아져야 한다. 그래서 모든 sub-sequences 를 foldRight 와 ++를 이용해서 결합할 필요가 있다. (xss: seq of seq)
(xss foldRight Seq[Int]())(_ ++ _)
// equvalently
xss.flatten
// so, 원래식 포함해서 아래와 같이 나타낼 수 있다.
((1 until n) map (i => (1 until i) map (j => (i, j)))).flatten
// 아래의 법칙을 이용하면
xs flatMap f = (xs map f).flatten
// 더 간단해질 수 있다.
(1 until n) flatMap (i => (1 until i) map (j => (i, j)))
// result
res0: scala.collection.immutable.IndexedSeq[(Int, Int)] = Vector((2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3), (6,4), (6,5))
// 두 합이 prime인것만 추려야함, 이전 챕터에서 만든 isPrime 이용
(1 until n) flatMap (i => (1 until i) map (j => (i, j))) filter (pair => isPrime(pair._1 + pair._2))
// result
res0: scala.collection.immutable.IndexedSeq[(Int, Int)] = Vector((2,1), (3,2), (4,1), (4,3), (5,2), (6,1), (6,5))For-Expression
for loop 에 대해서 알아보자
case class Person(name: String, age: Int)
// 20살 이상인 사람만 가져오고 싶을때
for (p <- persons if p.age > 20) yield p.name
// 아래와 같음
persons filter (p => p.age > 20) map (p = > p.name)기본적인 for loop 동작은 비슷하지만 결정적인 차이가 하나 있다. 보통 절차적 언어의 for loop 는 어떤 요소가 변할 수 있는 side effect 가 존재하지만 스칼라에서는 yield 키워드를 이용해서 iterable 객체를 생성한다.
for (s) yield efor-expression 을 위와같이 단순화 시킬 수 있다.
s is a sequence of generators and filters e is an expression whose value is returned by an iteration
- generator 의 p <- e 에서 p 는 하나의 패턴이고, e 는 컬렉션의 값이다.
- filter 의 f 는 boolean expression 이다.
- 몇개의 generator 가 있을때는 마지막이 처음보다 빠르다. why?
- ( s )는 { s }처럼 사용할 수도 있다.
example
이전에 보았던 문제를 for loop 를 이용해 다시 만들어 보자. 첫번째는 바로 전에 했던 두 수의 합이 prime 넘버인 것의 pair 를 구하는 함수
for {
i <- 1 until n
j <- 1 until i
if isPrime(i+j)
} yield (i, j)매우 심플해졌다.
두번째는 scalarProduct
def scalarProduct(xs: Vector[Double], ys: Vector[Double]): Double =
(for ((x, y) <- xs zip ys) yield x * y).sum따로 필터링할 조건이 없으므로 모든 요소에 대해서 적용한다.
6.3 Combinatorial Search Example
이번 챕터에서는 Set 에 대해 알아보자. Set 도 Seq 와 마찬가지로 Iterable 의 subclass 다. 그래서 Seq 에서 사용하는 대부분의 연산(map, filter 등)을 Set 에서도 동일하게 사용할 수 있다.
Sets vs Sequences
- Set 은 unordered 하다.
- Set 은 중복되는 element 를 가질 수 없다.
- Set 의 fundamental operation 은 요소가 해당 Set 에 포함되는지 확인하는 contains 다.
Example: N-Queens
예제를 살펴보자. 체스보드에 서로 위협이 되지 않는 8 개의 퀸을 놓는 방법을 찾는 문제이다. 다르게 말하면 같은 row, column, diagonal 에 둘 수 없는 문제와 같다.
알고리즘을 살펴보자.
- 사이즈 n 인 보드에 k-1 개의 퀸이 놓여진 모든 솔루션 추출
- 각 솔루션을 0 에서 n-1 까지의 columns 숫자로 구성된 리스트로 변환
- 리스트의 첫번째 요소는 k-1 번째 row 가 될 것이고, k-2, k-3 ...의 퀸을 붙여나간다.
- 각 솔루션의 하나의 element 와 함께 set of lists 로 만들어진다.
- kth 퀸을 놓아 가능한 모든 솔루션을 만들어낸다.
def queens(n: Int): Set[List[Int]] = {
def placeQueens(k: Int): Set[List[Int]] =
if (k == 0) Set(List())
else
for {
queens <- placeQueens(k - 1)
col <- 0 until n
if isSafe(col, queens)
} yield col :: queens
placeQueens(n)
}기본적인 뼈대는 위와 같다. placeQueens 함수를 재귀호출하여, 이전 단계의 퀸 리스트들을 이용해 다음 퀸들을 배치하는 형태다. 한 depth 씩 내려가다보면 마지막에는 빈 셋에 0 에서 n 까지 각각 배치될것이다. 그리고 1 개의 퀸이 배치된 list 들에다 하나씩 추가해가면 마지막에는 모든 퀸이 놓인 체스판이 완성될 것이다.
def isSafe(col: Int, queens: List[Int]): Boolean = {
val row = queens.length
val queensWithRow = (row -1 to 0 by -1) zip queens
queensWithRow forall {
case (r, c) => col != c && math.abs(col - c) != row - r
}
}기존 퀸 리스트에 새로운 퀸을 추가할 때 안전한지 검사하는 isSafe 함수다. case 부분만 유심히 보면 되는데, 각은 column 에 속하지 않으면서 대각선에 위치하지 않으면 safe 하다고 판단하고 퀸을 추가한다. 대각선상에 있는지는 컬럼의 차이와 행의 차이로 판단한다.
def show(queens: List[Int]) = {
val lines =
for (col <- queens)
yield Vector.fill(queens.length)("* ").updated(col, "X ").mkString
"\n" + (lines mkString "\n")
}
(queens(8) take 3 map show) mkString "\n"마지막은 리스트들로 되어 있는 퀸들을 실제 체스판에 올려놓은 것 처럼 출력해주는 show 함수를 이용한다. 결과는 아래와 같다.
res0: String =
* * X * * * * *
X * * * * * * *
* * * * * * X *
* * * * X * * *
* * * * * * * X
* X * * * * * *
* * * X * * * *
* * * * * X * *
* * * * * X * *
* * X * * * * *
X * * * * * * *
* * * * * * * X
* * * X * * * *
* X * * * * * *
* * * * * * X *
* * * * X * * *
* * * * X * * *
* X * * * * * *
* * * * * * * X
X * * * * * * *
* * * X * * * *
* * * * * * X *
* * X * * * * *
* * * * * X * *6.4 Maps
Map 에 대해서 알아보자. Map 은 다른 언어에서와 동일하게 Map[Key, Value]의 쌍으로 이루어져있다. 이때 Key, Value 는 숫자나 문자 등 어떤 타입이든 가능하다. 또한 Map[Key, Value]는 Key => Value 의 함수 타입으로 확장 가능하다. 즉, Key 파라미터를 이용하면 Value 를 구할 수 있다는 말과 같다.
// key를 이용해 value를 가져올때
capitalOfCountry("andorra") // exception 발생
// 대신에 get을 사용한다.
capitalOfCountry get "andorra" // NoneOption Type
Option 은 covariant 하기 때문에 Option[A] > Option[Nothing]이다. 즉 None
trait Option[+A]
case class Some[+A](value: A) extend Option[A]
object None extend Option[Nothing]패턴 매칭을 이용하면 아래와 같이 나타낼 수 있다.
def showCapital(country: String) = capitalOfCountry.get(country) match {
case Some(capital) => capital
case None => "missing data"
}Sorted and GroupBy
sql 쿼리의 opertaion 을 사용해보자.
// sorted
val fruit = List("apple", "pear", "orange", "pineapple")
fruit.sortWith (_.length < _.length) // List("pear", "apple", "orange", "pineapple")
fruit.sorted // List("apple", "orange", "pear", "pineapple")
// groupBy
fruit groupBy (_.head)
// Map(p -> List(pear, pineapple)),
// a -> List(apple),
// o -> List(orange))groubBy 명령은 식별 함수 f 에 따라 collection 의 map 을 만든다.
Polynoial Example
from exponents to coefficient 방식으로 map 을 만든다.
class Poly(val terms: Map[Int, Double]) {
def + (other: Poly) = new Poly(terms ++ other.terms)
override def toString =
(for ((exp, coeff) <- terms.toList.sorted.reverse) yield coeff+"x^"+exp) mkString " + "
}
val p1 = new Poly(Map(1 -> 2.0, 3 -> 4.0, 5 -> 6.2))
val p2 = new Poly(Map(0 -> 3.0, 3 -> 7.0))
p1 + p2두 다항식을 더하는 함수를 작성해보자. 양쪽 다항식에 exponents 가 같은 coefficient 끼리 더해주고 나머지 exponents 들을 합쳐주면 두 다항식의 합이 완성된다. 일단 말은 어렵지 않다. 하지만 위의 식은 아래처럼 잘못된 결과가 도출된다.
p1: Poly = 6.2x^5 + 4.0x^3 + 2.0x^1
p2: Poly = 7.0x^3 + 3.0x^0
res0: Poly = 6.2x^5 + 7.0x^3 + 2.0x^1 + 3.0x^0왜 그럴까?? 맵끼리 concatenating 할때는 아마 같은 키의 value 를 합치는게 아니라 뒤에 나오는 map 의 key 의 value 로 대체하기 때문에 이렇게 나오는 것이다. 다음과 같이 바꿔보자.
def + (other: Poly) = new Poly(terms ++ (other.terms map adjust))
def adjust(term: (Int, Double)): (Int, Double) = {
val (exp, coeff) = term
terms get exp match {
case Some(coeff1) => exp -> (coeff + coeff1)
case None => exp -> coeff
}
}뒤에 오는 other 에 adjust 함수를 매핑해보자. adjust 함수는 other 의 term 하나를 뽑아다가 terms 에 해당 exponent 가 있는지 확인하고 있으면 terms 와 other(term)의 coefficient 를 더해준다. 만약 없다면, othe 의 coeff 를 그대로 리턴한다. 결과를 보자.
p1: Poly = 6.2x^5 + 4.0x^3 + 2.0x^1
p2: Poly = 7.0x^3 + 3.0x^0
res0: Poly = 6.2x^5 + 11.0x^3 + 2.0x^1 + 3.0x^0Default Values
심플한 방법이 있었다. withDefaultValue operation 을 이용하면 위의 함수를 좀더 간단하게 만들 수 있다. withDefaultValue 를 이용해 좀더 개선해보자.
class Poly(terms0: Map[Int, Double]) {
def this(bindings: (Int, Double)*) = this(bindings.toMap)
val terms = terms0 withDefaultValue 0.0
def + (other: Poly) = new Poly(terms ++ (other.terms map adjust))
def adjust(term: (Int, Double)): (Int, Double) = {
val (exp, coeff) = term
exp -> (coeff + terms(exp))
}
override def toString =
(for ((exp, coeff) <- terms.toList.sorted.reverse) yield coeff+"x^"+exp) mkString " + "
}
val p1 = new Poly(1 -> 2.0, 3 -> 4.0, 5 -> 6.2)
val p2 = new Poly(0 -> 3.0, 3 -> 7.0)
p1 + p2
p1.terms(8)크게 두가지가 바뀌었다. 첫째는 Poly 클래스의 parameter 에 default value 를 적용해주어 adjust 에서 패턴매칭하는 수고로움을 줄여 주었다. (exp -> (coeff + terms(exp))) 그리고 둘째는 새로운 Poly 를 생성할 때, Map 타입을 지정해 주지 않아도, 생성자에서 (Int, Double)이 sequencial 하게 들어오면 이를 Map 으로 바꿔주도록 하였다.
Exercise
위에서 보았던 '++' 연산과 foldLeft 를 이용한 연산중 어느것이 더 효율적일까?
def + (other: Poly) =
new Poly((other.terms foldLeft terms)(addTerm))
def addTerm(terms: Map[Int, Double], term: (Int, Double)): Map[Int, Double] = {
val (exp, coeff) = term
terms + (exp -> (coeff + terms(exp)))
}fold 를 이용하면 위에서처럼 Map 을 생성하여 각 exponent 를 비교해서 값을 넣는게 아니라 기존부터 있던 terms 에다 즉각적으로 추가하기 때문에 ++보다 더 효율적이라 할 수 있다.
6.5 Putting the Pieces Together
전화번호를 문자로 바꾸는 예제를 살펴보자. 참고로 해당 예제는 파이썬과 같은 스크립트 언어에서는 100 라인 정도, 그외에 일반적 목적의 프로그래밍 언어에서는 200~300 라인정도의 코드가 나왔다고 한다.
val mnemonics = Map(
'2' -> "ABC", '3' -> "DEF", '4' => "GHI", '5' -> "JKL",
'6' -> "MNO", '7' -> "PQRS", '8' -> "TUV", '9' -> "WXYZ")위와 같이 각 번호가 몇개의 문자열로 매핑되어 있다. 해당 숫자가 나왔을때 매핑된 문자열 중에 하나의 문자를 선택해서 출력해준다는 얘기다.
예를 들어 "7225247386"를 convert 해보면 그 중 하나가 "SCALAISFUN"(Scala is fun)이 된다.
전체코드는 다음과 같다.
val in = Source.fromURL("http://lamp.epfl.ch/files/content/sites/lamp/files/teaching/progfun/linuxwords.txt")
val words = in.getLines.toList filter (word => word forall (chr => chr.isLetter))
val mnem = Map(
'2' -> "ABC", '3' -> "DEF", '4' -> "GHI", '5' -> "JKL",
'6' -> "MNO", '7' -> "PQRS", '8' -> "TUV", '9' -> "WXYZ")
val charCode: Map[Char, Char] =
for ((digit, str) <- mnem; ltr <- str) yield ltr -> digit
/**
* 파라미터로 들어온 문자열을 charCode로 변경함
* @param word
* @return
*/
def wordCode(word: String): String =
word.toUpperCase map charCode
wordCode("Java") // res0: String = 5282
/**
* A map form digit strings to the words that represent them,
* e,g. "5282" -> List("Java", "Kata", "Lava", ...)
* Note: A missing number should map to the empty set, e,g. "11111" -> List()
*/
val wordsForNum: Map[String, Seq[String]] =
words groupBy wordCode withDefaultValue Seq()
/**
* Return all ways to encode a number as a list of words
*/
def encode(number: String): Set[List[String]] =
if (number.isEmpty) Set(List())
// 1 to number.length는 IndexedReq 타입이므로 Set 타입으로 변경해준다
else {
for {
split <- 1 to number.length
word <- wordsForNum(number take split)
rest <- encode(number drop split)
} yield word :: rest
}.toSet
encode("7225247386")
def translate(number: String): Set[String] =
encode(number) map(_ mkString " ")
translate("7225247386")지금까지 살펴본 스칼라 collection 은 아래와 같이 정리 할 수 있다.
- easy to use: few steps to do the job.
- concise: one word replaces a whole loop.
- safe: type checker is really good at catching errors.
- fast: collection ops art tuned, can be parallelized.
- universal: one vocabulary to work on all kinds of collections.